Programarea Calculatoarelor, seria CC

Laborator 5

Definirea şi utilizarea de funcţii

În acest laborator veţi învăţa să:


Problema 1 - problemă rezolvată.

Scrieţi o funcţie care să calculeze numărul de cifre ale unui număr întreg nenul dat ca parametru. În funcția main() citiți un număr de la tastatură şi afişați rezultatul apelului funcţiei. Antetul funcţiei trebuie să respecte următorul format:

int nrcf(long n)

Rezolvare:

Programul C care implementează cerința problemei de mai sus va fi:

 1 #include <stdio.h>
 2
 3 int nrcf(long n)
 4 {
 5     int nr = 0; /* declar un contor in care sa numar cifrele */
 6     while (n) /* cat timp mai pot obtine o cifra */
 7     {
 8         n = n/10; /* o trunchiez pe ultima */
 9         nr++; /* incrementez contorul */
10     }
11     return nr; /* functia intoarce numarul de cifre */
12 }
13
14
15 int main(void)
16 {
17     long N;
18     printf("N = "); /* afisam un mesaj pentru utilizator */
19     scanf("%ld", &N); /* citim numarul introdus de la tastatura */
20
21     printf("Numarul %ld are %d cifre!\n", N, nrcf(N)); /* afisez numarul de cifre */
22
23     return 0;
24 }

Exemplu:

Intrare Ieşire
1325135 7
274 3
666013 6

Problema 2.

Scrieţi o funcţie care să verifice dacă un număr întreg n conţine cifra c. Numerele n şi c sunt date ca parametri. Antetul funcţiei trebuie să respecte următorul format:

int cifra(int n, int c)

Exemplu:

Intrare Ieşire
13584 3 DA
100111 0 DA
666013 8 NU

Problema 3.

Ipoteza lui Goldbach: Orice număr par se poate exprima printr-o sumă de două numere prime, nu neapărat distincte.

A. Scrieţi o funcţie care să verifice dacă un număr întreg este prim sau nu. Funcţia va returna valoarea 1 dacă argumentul este număr prim şi 0 în caz contrar. Antetul funcţiei trebuie să respecte următorul format:

int prim(int n)

B. Scrieţi un program care verifică ipoteza lui Goldbach prin afişarea tuturor descompunerilor distincte(de ex. nu se vor afișa și "5+7" și "7+5") posibile în sumă de numere prime ale unui număr citit de la tastatură. Programul va apela funcţia prim.

Observaţie: Se va considera pentru această problemă că numărul 1 este prim.

Exemplu:

Intrare Ieşire
12 1+11
5+7

Problema 4.

Se citesc de la tastatură patru numere întregi reprezentând două fracţii x1/y1 şi x2/y2. Aduceţi fracţiile la acelaşi numitor (cel mai mic posibil) folosind o funcţie care calculează cel mai mic multiplu comun a două numere întregi. Antetul funcţiei trebuie să respecte următorul format:

int cmmmc(int a, int b)

Hint: cmmmc(a, b) = (a * b) / cmmdc(a, b)

Exemplu:

Intrare Ieşire
1 2
1 11 		11/22
2/22

Problema 5.

Să se scrie un program pentru calculul sumei seriei Taylor pentru funcţia ex până la un termen dat:

ex = 1 + x/1! + x2/2! + x3/3! + ... + xn/n!

Se vor defini şi utiliza următoarele funcţii:

  1. Funcţie pentru calculul sumei seriei Taylor în punctul x până la un termen n dat:

    double taylor(double x, int n)

  2. Funcţie pentru calculul factorialului unui număr întreg:

         int factorial(int n)

  3. Funcţie pentru calculul puterii întregi a unui număr dat:

         double putere(double x, int n)

Comparaţi rezultatul obţinut cu rezultatul funcţiei exp(x) şi cu rezultatul funcţiei pow(2.718,x).

Problema 6.

Se citesc n puncte de la tastatură, date prin coordonatele lor: xi, yi, i=1,n. Să se afişeze perechea de puncte între care distanţa este maximă (dacă există mai multe astfel de perechi, se poate afişa oricare dintre ele), precum şi această distanţă. Se va defini şi folosi o funcţie pentru calculul distanţei dintre două puncte în plan, care trebuie să respecte următorul antet:

float dist(int x1, int y1, int x2, int y2)

Exemplu:

Intrare Ieşire
4
0 0
0 1
1 0
1 1 		[(0,0);(1,1)] formeaza distanta maxima 1.414214
3
2 -2
3 4
7 8
 [(2,-2);(7,8)] formeaza distanta maxima 11.180340

Problema 7.

Scrieţi o funcţie care sortează cifrele unui număr astfel:

  1. descrescător, dacă numărul conţine cifra 0
  2. crescător, dacă numărul nu conţine cifra 0
Funcţia trebuie să respecte următorul antet

int transforma(int n)

HINT! Pentru a sorta cifrele, cea mai simpla metoda este sa folositi un vector cu 10 elemente in care sa memorati pentru fiecare cifra, de cate ori apare aceasta in numar. Pentru a afisa numarul sortat, trebuie sa parcurgeti vectorul si sa afisati cifrele in ordine crescatoare/descrescatoare conform cu numarul lor de aparitii.

Exemplu:

Intrare Ieşire
19430123 94332110
2534562 2234556

Problema 8.

Scrieţi o funcţie care caculează aria intersecţiei a două dreptunghiuri, date prin coordonatele colţurilor stânga-sus şi dreapta-jos. Coordonatele sunt numere întregi pozitive. Funcţia trebuie să respecte următorul antet:

int arie_intersectie(int x11, int y11, int x12, int y12, int x21, int y21, int x22, int y22)

Exemplu:

Intrare Ieşire
1 10 5 5
2 7 4 4 		4
1 3 3 1
2 4 4 3 		0

Probleme suplimentare

Problema 1.

Să se scrie o funcţie care determină ultima cifră diferită de 0 a factorialului unui număr natural dat mai mic decât 300. Funcţia trebuie să respecte următorul antet:

int last_nonzero_digit(int n)

Observaţie: Nu încercaţi să calculaţi direct numărul n! deoarece rezultatul va creşte rapid depăşind limita maximă a oricărui tip de dată întreg.

Exemplu:

Intrare Ieşire
7
 4

Problema 2.

Să se scrie o funcţie care determină aria reuniunii a trei dreptunghiuri date prin coordonatele întregi ale colţurile stânga-sus şi dreapta-jos.

Observaţie: Folosiţi funcţia definită în problema 8.

Exemplu:

Intrare Ieşire
0 0 8 6
4 2 11 9
2 -2 6 4 		89

Explicaţie:

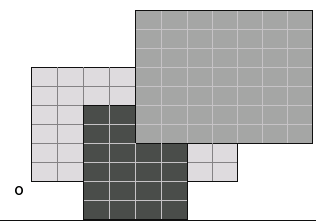
La această problemă puteți să vă testați sursele folosind evaluatorul de pe inforena. Problema se numește Reuniune și se gasește aici.