Să luăm un exemplu cât mai simplu de problemă. Vrem să scriem un program care să ne calculeze automat valorile unei funcţii matematice:

F(x) =

• x²-2 , dacă x<0
• 3, dacă x=0
• x+2, dacă x>0

Pentru rezolvarea unei probleme, trebuie să parcurgem următorii paşi:

1. Elaborarea algoritmului de rezolvare al problemei. (* Un algoritm reprezintă o secvență finită de pași a căror execuție în ordine, duce la rezlvarea unei clase de probleme ).
2. Transpunerea algoritmului în limbaj de programare.
3. Testare. (și în caz de erori, se revine la pasul 1)

Trebuie să precizăm că există două tipuri de obiecte cu care lucrează algoritmii:

1. variabile: care au nume unic, și conținut diferit în funcție de momentul de execuție. Ele sunt caracterizate prin:
   • Nume
   • Tip
   • Valoarea la un moment dat (depinde de momentul execuției)
   • Locul în memorie (adresa)
2. date: acestea pot fi de asemenea de două tipuri
   • De intrare: sunt valori pe care algoritmul de primește din exterior
   • De ieșire: sunt rezultatele pe care le calculează algoritmul.

Atunci când vorbim despre instrucțiunile specifice programării structurate, trebuie să amintim de teorema de structură a lui Bohm și Jacopini: Orice algoritm poate fi compus din numai trei structuri de calcul:

• Structuri secvențiale = secvențe - în care instrucțiunile se execută în ordine
• Structuri alternative = decizii - decid dacă să se continue execuția pe o ramură sau alta
• Structuri repetitive = cicluri - execuția repetată a unui corp de instrucțiuni

Fiecare dintre aceste structuri are o singură intrare și o singură ieșire.

Există mai multe tipuri de instrucțiuni secvențiale:

• Atribuirea: operația prin care unei variabile a i se dă o valoare.
  
• Operațiile de intrare/ieșire (I/O): se citesc valori de la tastatură sau se afișează valori pe ecran.
  

În pseudocod:

• a = 3;
• citeste a;
• scrie a;

Decizia implementează o întrebare ridicată de programator la un moment dat în program. În funcție de răspuns (care poate fi de tipul DA/NU se poate continua execuția programului în două moduri.

În pseudocod:

dacă (condiție) atunci
    instrucțiuni-adevărat;
altfel
    instrucțiuni-fals;

Structurile repetitive se folosesc pentru a exprima faptul că un anume corp de instrucțiuni trebuie repetat de mai multe ori. Exsită trei tipuri de cicluri (structuri repetitive):

• I) Cu condiție inițială
• II) Cu condiție finală
• III) Cu contor

I) Ciclul cu condiție inițială: este alcătuit dintr-o condiție logică urmată de un bloc de instrucțiuni. Dacă condiția este falsă, se sare peste blocul aferent de instrucțiuni, iar în caz contrar, se repetă blocul de instrucțiuni atâta timp cât condiția rămâne adevărată.

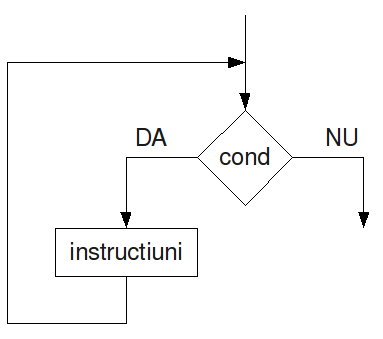
În pseudocod:

cât timp (conditie)
    instrucțiuni;

II) Ciclul cu condiție finală: este alcătuit dintr-un bloc de instrucțiuni, urmat de o condiție logică. Dacă condiția este falsă, se continuă execuția programului, iar în caz contrar, se repetă blocul de instrucțiuni atâta timp cât condiția rămâne adevărată. Spre deosebire de structura repetitivă cu condiție inițială, se garantează că blocul de instrucțiuni se va repeta cel puțin o dată.

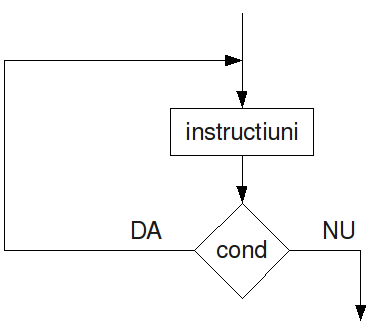
În pseudocod:

execută {
    instrucțiuni;
} atata timp cât (condiție);

II) Ciclul cu contor: este alcătuit dintr-un bloc de instrucțiuni, care are atașat un contor. Contorul primește la început o valoare inițială, se execută blocul de instrucțiuni și se incrementează valoarea contorului. Execuția și incrementrea se repetă atâta timp cât contorul nu ajunge la valoarea finală.

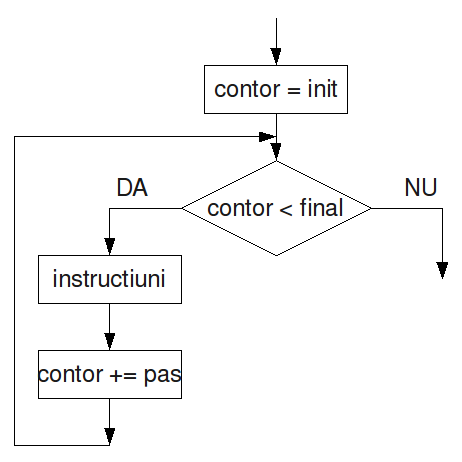
În pseudocod:

pentru contor de la valoarea-inițială pana la valoarea-finală cu pasul pas
    instrucțiuni;

Structurile auxiliare se folosesc pentru a specifica:

• I) Începerea execuției unui algoritm
• II) Finalizarea execuției unui algoritm
• III) O serie de prelucrări nedetaliate

În pseudocod:

start
stop.
prelucrări;

Observații

• Un algoritm poate să aibă doar un singur bloc start
• Un algoritm trebuie să aibă cel putin un bloc stop
• Orice bloc de tip prelucrări nedetaliate poate fi înlocuit cu o schemă logică echivalentă

1. Interschimbul valorilor a două variabile a şi b.
2. Rezolvarea ecuaţiei de gradul 2: ax²+bx+c=0.
3. Să se afişeze în ordine crescătoare valorile a trei variabile: a, b şi c.
4. Să se calculeze şi să se afişeze suma: S= 1 + 1*2 + 1*2*3 + ... n!.
5. Să se calculeze şi să se afişeze suma cifrelor unui număr natural n.
6. Să se calculeze şi să se afişeze inversul unui număr natural n.
7. Să se afişeze dacă un număr natural dat n este prim.
8. Să se afişeze primele n numere naturale prime.
9. Să se descompună în factori primi un număr dat n.
10. Să se calculeze valoarea minimă, respectiv maximă, dintr-o secvenţă de n numere reale.
11. Să se afişeze toate numerele naturale mai mici decât 1000 care se pot scrie în două moduri diferite ca sumă de pătrate.
12. Se dă o secvenţă de n numere întregi pozitive. Să se afişeze cele mai mari numere de 2 cifre care nu se află în secvenţa respectivă.
13. Se dă o secvenţă de n numere întregi, ale căror valori sunt cuprinse în intervalul [0,100]. Să se afişeze valorile care apar cel mai des. (se vor folosi vectori)